第5章 西洋数学の導入
ここでは視点を変えて、和算と西洋数学との関係を述べます。
ともすると和算は、日本独自の数学であることのみが強調されて、外国の数学の影響やそれとの交渉はほとんど無かったかのように語られることがしばしばです。外国の数学といっても中国数学からの影響があったことは容易にわかるのですが、西洋の数学となるとそれがどの程度導入されたのか想像が付かないというのが実状でしょう。
実際の様子を探ると、常にというわけではありませんが、機会があれば西洋の数学が日本に流入するルートは開けていました。しかし、この流入する内容は決して体系的なものではなく、その時々に必要とされていたもの、偶然日本にもたらされたものであった、ということが現代社会の文化交流の形式と大いに異なっています。
(1) 17世紀中頃
17世紀中頃に幕府が国絵図を大名たちに命じて作らせていた際、幕府の責任者である井上政重は、その部下たちにオランダ人から数学(幾何学)を学ばせています。地図作成のために必要な知識であったと思われます。このことは、長崎出島のオランダ商館長日記に明記されています(慶安元年(1648)のこと)。
しかし、この西洋の幾何学の知識はどうやら断片的なものに終わったらしく、その後の和算書などに影響を見て取ることはできません。
(2) 吉宗の治世下:禁輸緩和
次に大々的に西洋の数学が導入されたのは、江戸時代のちょうど中頃、8代将軍吉宗の治世(1716-1745)の時期に当たります。
吉宗はいわゆる享保の改革を進める過程で様々な施策を打ち出しますが、それらは決して財政方面の事柄ばかりではなく、意外にも医療や科学技術、産業全般にわたる内容も取り上げられました。朝鮮人参の国産化、全国の産物調査などです。暦法改革もその一つでした。
吉宗は将軍就任直後から、天文暦学の話題に関心を寄せていたことがうかがえます。第2章でも述べた建部賢弘(1664-1739)を重用し、暦学や地図に関する仕事を任せています。特に暦法に関しては、中国清王朝が西洋の天文学に基づいて暦を作成していることを知り、それに関連する本を輸入させて建部と中根元圭(1662-1733)に研究を命じています。この当時、ヨーロッパ人が書いた書物の中でも、キリスト教宣教師による著作は内容の如何を問わず、輸入禁止措置が取られていたわけですが、吉宗は西洋の暦法を知るためにこの禁輸措置を緩和しました。すなわち、たとえキリスト教宣教師が書いた書物であっても、純粋に科学技術の方面の著作であれば輸入してもよいというものでした。注意しなければいけない点は、ここで想定されていたのが中国語に翻訳された西洋の著作だということです。いまだヨーロッパの言語を自由に操れる人は日本にはほとんどいなかったので、むしろ幕府が警戒をしていたのは中国語によるキリスト教の流布でした。

『人参耕作記』から、移植された朝鮮人参
国立国会図書館デジタルコレクション
(3) 吉宗の治世下:改暦の取り組み
さて、この緩和措置によってもたらされた書物の代表は、西洋の数学と暦学を取り込んでまとめられた梅文鼎(1633-1721)の『暦算全書』でした。この本を建部と中根が研究したわけです。この中に紹介されている内容で、当時の日本人に取り込まれたのは、今でいう三角関数(サイン、コサイン、タンジェント、......)の数表でした。これ以後、日本人の数学者たちはこの方面の研究も精力的に進め、数表の精密化に努力を傾けます。
話を吉宗周辺に戻すと、建部や中根に研究を進めさせる一方、吉宗は幕府天文方のてこ入れも進めます。建部と中根は改暦に至る前に没してしまいますが、その後を受けた天文方のメンバーは望遠鏡などを用いた天文観測を進め、準備を進めます。山路主住(1704-1773)・之徽(1729-1778)親子は、幕府天文方に属した関流の和算家ですが、この時期、吉宗に命ぜられてオランダ人から天文暦学に関する知識を学ばされています。
このようにして進められた吉宗の改暦事業ですが、残念ながら、吉宗はその成果を見る前に没してしまいます。その没後すぐに作られたのが宝暦暦でしたが、吉宗の死没やその他様々な理由により、この暦は不完全な物となってしまいました。しかし、この宝暦暦を改訂していく過程で、幕府天文方は吉宗の敷いた路線である西洋天文学の導入を更に進めていくことになります。それはすなわち、天文学周辺にある西洋数学の知識も取り入れることにつながったわけです。
- コラム 三角関数表(難易度2)
-
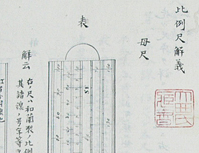
西欧の計算尺(比例尺)の使用法をまとめたもの。吉宗の時代に導入された西洋数学の一端を示している。
『比例尺解義』の拡大画像を表示
『比例尺解義』(個人蔵) 
宝暦暦にかかわった人物の書で、天文学と数学、暦学の関係について語った部分
『数学夜話』のライブラリへ移動
西村遠里 『数学夜話』
国立国会図書館デジタルコレクション
(4) 様々な西洋数学知識
三角関数表の他に和算家が取り入れた西洋数学の内容として、対数表、球面三角法があります。対数表は現在でも高等学校で教えられていますが、それと同じ物が江戸時代に輸入されています。球面三角法は、現在の日常生活ではあまりお目にかかりませんが、天文学や地球規模で移動するような航海術では必要になる算法です。球面上に描く三角形では、平面の場合とは異なる公式が必要になるのです。
ヨーロッパの幾何学の知識も、18世紀以降、日本に入っています。一例を挙げると、仙台藩の和算家である戸板保佑(1708-1784)の手元にあった中国書『数度衍』にはヨーロッパの幾何学の体系が中国語で記され、まとめられていました。戸板はこの本から大きな影響を受けていたことがわかっています。
幕末になると、この西洋数学導入の動きは加速していきます。天文暦学ばかりではなく、様々な分野に応用される数学が日本人の目にとまるようになりました。砲術、築城術、造船術、等々、欧米の軍事技術の核をなす数学が紹介されることになります。
ここまでの説明でおわかりの通り、江戸時代における西洋数学の導入は、数学そのものというよりも何らかの応用や実践を前提とし、それに必要な数学として取り入れられた物がほとんどです。ヨーロッパの最先端の数学(微積分や代数学)が体系的に取り込まれたわけでないことは注意すべきでしょう。技術に必要な数学、そして数学そのものを目的として研究する数学という二つの側面をともに認知し、本格的に取り込むことになるのは、日本では明治初期以降のことになります。
-

西欧の航海術に必要な基本知識、測量法を備忘的にまとめた一書。著者・年代不詳。
『泰西測量器』の拡大画像を表示
『泰西測量器』(電気通信大学蔵) -
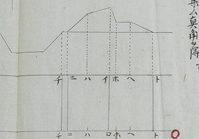
幕末にオランダの軍事技術書(原典未詳)から築城に必要な知識の図を抜粋した一枚
『築城新法』の拡大画像を表示
『築城新法』(電気通信大学蔵)


