第5章 西洋数学の導入
コラム 三角関数表(難易度2)
三角関数は直角三角形に対して考えられる6種類の比の間の関係を扱う三角法がその起源で、角度に比の値を対応させる6種類の関数です。三角法は英語ではtrigonometry といい、三角形の測量という意味です。四千年前の古代エジプトで、すでにその萌芽が見られ、バビロニアやギリシアの天文学にもその考え方が見られます。6世紀インドで書かれた『アールヤバティーヤ』という本は様々な角度の正弦(sin)値を計算する方法を述べており、はっきりと三角関数としてとらえられています。インドの三角関数がアラビア経由でヨーロッパに伝わったと考えられており、現在使われているsin、cos、tanといった表記法はヨーロッパで考え出されました。我が国にはオランダ語の数学書・天文学書や中国に伝わったヨーロッパの数学や天文学の漢訳書(『崇禎暦書』など)を通じて伝わりました。主に天文計算、測量術、航海術で使われ、ヨーロッパの物理学の本に頻出します。三角関数は角度に数字を対応させる関数ですから、角度の概念がないと生まれません。ところが、和算では角度の概念がありませんでした。方角は十二支に対応させて示していましたが、数値化はされていないので、中間の方角を正確に表現できません。角度が使われたのは、天文、測量、航海術の分野においてのみでした。
三角関数表は決められた角度における正弦(sin)や余弦(cos)、正接(tan)の値を表にしたものです。古代ギリシアのプトレマイオス(c.85-c.165)は『アルマゲスト』の中で正弦の表を作成しています。正確には斜辺(半径)の長さが60の直角三角形(円)のある角度の2倍(中心角)に対する対辺の長さの2倍(弦)の表で、弦の表(chord table)と呼ばれます。
弦の表と三角関数の関係がわかる図
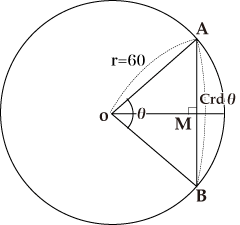 プトレマイオスの弦の表は∠AOBに対応する弦ABの長さCrdθを表にしたもので、OA=OB=60として計算しています。例えば
プトレマイオスの弦の表は∠AOBに対応する弦ABの長さCrdθを表にしたもので、OA=OB=60として計算しています。例えば
![]() という数値となっています。
という数値となっています。
一方、sin xは、OA=1の時にsin∠AOM=AMと定義されていますので、Crd θ=2×60 sin θ/2という関係があります。Crd 60°から120 sin 30°=60、すなわち
![]() という数値となっています。
という数値となっています。
となり、Crd 90°から120 sin 45°=84.85277…すなわちsin 45°=0.7071064…となります。
この表において、角度を半分にして、弦の長さを120で割ると現在の正弦表となります。プトレマイオスはこの表を作るのに用いた計算法についても『アルマゲスト』の中で説明しており、30°、45°、60°のような計算しやすい角度から始めて、36°、72°は正五角形、正十角形の辺の長さとして計算します。さらにトレミーの定理と呼ばれる定理を使って、二つの角度の和と差の角の弦の長さが計算できる公式を導き、また、ある角度の半分の角度の弦の長さを計算する式を導きます(角の和と差と弦の長さ)。すると12°、6°、3°、1.5°等々の正弦が計算されます。次に0.5°の正弦について、それは0.75°の正弦の2/3倍より大きく、0.375°の正弦の4/3倍より小さいことを示し、さらにこの2つの数値が等しいことを計算しています。こうしてプトレマイオスは中心角が0°から180°までの弦の長さを0.5°きざみで(したがって、0°から90°までの正弦を0.25°きざみで)表にしました。
この表で、例えば中心角120°の値を見ると、中心角 120°の弦の長さは 103;55,23 ![]() 、角が
、角が![]() 増加するごとに弦の長さは ;0,31,18 ずつ増加するという補間法が記されています。面白いのは長さの小数部分が60進法で記されていることで、半径を60としているのも補間法の計算を簡単にするためです。ちなみに中世ヨーロッパでは60進法の小数1桁目はpartes minutae primae、小数2桁目はpartes minutae secundae と呼ばれました。minutus は「細分された」という意味の形容詞です。時間や角度の第一細分を「分」(minute)と、第二細分を「秒」(second)と呼ぶのはここからきています。
増加するごとに弦の長さは ;0,31,18 ずつ増加するという補間法が記されています。面白いのは長さの小数部分が60進法で記されていることで、半径を60としているのも補間法の計算を簡単にするためです。ちなみに中世ヨーロッパでは60進法の小数1桁目はpartes minutae primae、小数2桁目はpartes minutae secundae と呼ばれました。minutus は「細分された」という意味の形容詞です。時間や角度の第一細分を「分」(minute)と、第二細分を「秒」(second)と呼ぶのはここからきています。
それではこの表からsin 60°を計算してみましょう。sin 60°は半径1の円での中心角 120°の弦の長さの半分ですので、弦の長さ
![]()
を120で割りますと
![]()
となり、![]() と一致していることがわかります。
と一致していることがわかります。
インドではこの対辺 (弦の半分) の長さをjya と呼び、それがアラビア世界では翻字されてjaib と呼ばれました。この音はアラビア語で「入江」を意味しますので、12世紀にラテン語に翻訳された時、「入江」のラテン語「sinus」が使われました。このようにしてヨーロッパで正弦をsinusやsine と呼ぶ三角法の研究が始まりました。特に天文学者たちが熱心に研究し、レギオモンタヌスの名で知られるヨハン・ミューラー(1436-1476)のDe triangulus omnimodis (1464年成立)は最初の三角法の教科書であり、Tabula directionum (1490)は刊行された最初の三角関数表です。また、1596年に刊行されたG.レティクス(1514-1576)のOpus palatinumは1,400ページを超す三角法と三角関数表の集大成となりました。また、コペルニクスやケプラーの天文学は三角関数表を利用することで革新的な理論が組み立てられたということです。
我が国での最初の三角関数表は建部賢弘(1664-1739)の『算暦雑考』であるといわれます。建部賢弘は円周率の計算を行ったことで有名ですが、その数値を用いて1度毎に![]() sin x の値を小数点以下11桁まで計算した半弦表を作りました。建部は1度を1限と呼んでおり、直径が1尺の円で計算しましたので、半弦の長さが(1/2)sin x尺となっています。建部は図のような半背(弧)、矢、半弦の長さを1限おきに計算した表を作りました。この本は佐藤健一『建部賢弘の「算暦雑考」』(1995)に復刻されています。
sin x の値を小数点以下11桁まで計算した半弦表を作りました。建部は1度を1限と呼んでおり、直径が1尺の円で計算しましたので、半弦の長さが(1/2)sin x尺となっています。建部は図のような半背(弧)、矢、半弦の長さを1限おきに計算した表を作りました。この本は佐藤健一『建部賢弘の「算暦雑考」』(1995)に復刻されています。
-
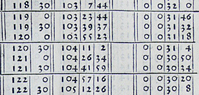
0.5°きざみの弦の表の中心角120°付近の値
Ptolemy: Almagestの拡大画像を表示
Ptolemy: Almagest (Venice, 1515)
建部の半背、矢、半弦の図
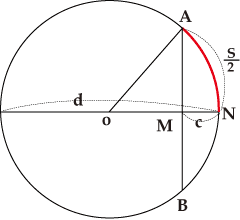 建部は直径dと矢cから半背
建部は直径dと矢cから半背![]() を求める公式、半背
を求める公式、半背![]() と直径dから矢を求める公式などを見つけ、直径が1尺の円について、角度1°の弧の長さを0.00872664626として、1°の半弦の長さAMを0.0087262032187、2°の半弦の長さを0.0161679…、…30°の半弦の長さを0.25、45°の半弦の長さを0.35355339…、60°の半弦の長さを0.433012701…、などと計算しました。
と直径dから矢を求める公式などを見つけ、直径が1尺の円について、角度1°の弧の長さを0.00872664626として、1°の半弦の長さAMを0.0087262032187、2°の半弦の長さを0.0161679…、…30°の半弦の長さを0.25、45°の半弦の長さを0.35355339…、60°の半弦の長さを0.433012701…、などと計算しました。
これは直径が1の時の半弦の長さですので、正弦(sin)はその2倍の値となります。
我が国で実際に使われた三角関数表はヨーロッパの三角関数表を漢訳したもので、割円八線表と呼ばれました。八線とは図のような8種類の値で、正弦(sin x)、余弦(cos x)、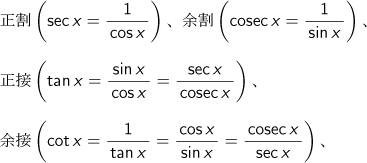
正矢(1-cos x)、余矢(1-sin x)の8つを、そう呼んでいます。
八線の図示
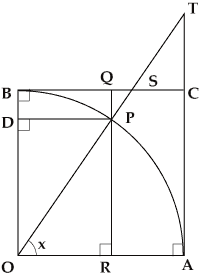 図でOA=OP=OB=半径=1、
図でOA=OP=OB=半径=1、
正弦=PR=sin x、余弦=DP=cos x
正接=AT=tan x、
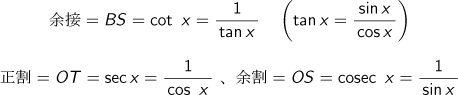
正矢=RA=1-cos x、余矢=QP=1-sin x
を表わします。ピタゴラスの定理からsin2x+cos2x=1となります。
角度の単位は直角を90度としますが、1度を60等分してそれを1分とした表と1度を100等分してそれを1分とした表の2種類があります。図にあります森正門の『割円表』(1857)は1度を60分としていますが、渋川景佑(1787-1856)の『新法暦書 続編』(1846)では1度を100分としています。
割円八線表は日本地図作成で有名な伊能忠敬(1745-1818)が測量時に携帯していたことで有名です。三角関数表の測量、地図製作での利用についてはコラム 「測量の方法」をご覧ください。
天文学では球面三角法を利用するので、三角関数の掛け算が多く出てきます。この掛け算を足し算に変える三角関数の対数表も作られており、この表も我が国に輸入され、紹介されました。また、三角関数表は円を三等分する弦の長さを求める時に出てくるsin x = ax+b のような超越方程式を解く場合に必要になります。現在は三角関数表は表計算ソフトに内蔵されているので、円の三等分の問題をエクセルで解くこともできます。これについては腕試し問題Q15をご覧ください。
-

30度付近の正弦、60度付近の余弦
『割円表』の拡大画像を表示
森正門『割円表』


