第5章 西洋数学の導入
コラム 角の和と差と弦の長さ(難易度2)
プトレマイオスは角の和や差の弦の長さを計算しました。トレミーの定理(トレミーPtolemyとはプトレマイオスの英語形)を使うと、ある二つの角度の弦の長さから、その二角の和の角度と差の角度の弦の長さを計算することができます。ここではまず、『アルマゲスト』にあるやり方で、その公式を証明しましょう。
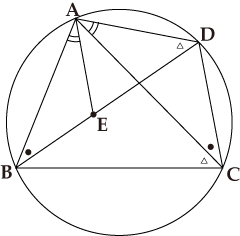
トレミーの定理
図でBD上に点Eを∠BAE=∠CADとなるようにとります。△ABEと△ACDは二角が等しいので相似となり、AB/BE=AC/CD すなわちAB×CD=AC×BE となります。同様に△ABCと△AEDも二角が等しいので相似となり、AD/DE=AC/BC すなわちAD×BC=AC×DE となります。この2式の両辺を足しますと AB×CD+AD×BC=AC×(BE+DE)=AC×BD となります。特に四角形ABCDがAB=CD,AD=BC,∠DAB=∠ABC=∠BCD=∠CDA=90°という長方形の場合、AB×CD+AD×BC=AC×BD はピタゴラスの定理のことになります。
このAC×BD=AB×CD+AD×BC という公式を図AのようにBCが長さ2Rの直径となるようにすると、Crd(α)×Crd(180°-β)=2R×Crd(α-β) + Crdβ×Crd(180°-α) すなわち
Crd(α-β) = Crd(α)×Crd(180°-β)/2R - Crdβ×Crd(180°-α)/2R
という二つの角の差の弦の長さを計算する公式が得られます。これはsinx=Crd(2x)/2Rという関係から、三角関数の加法定理 sin(x-y)=sin x×cos y-cos x×sin y を意味しています。
二つの角の和の弦の長さについては図Bを使うと
Crd(180°-α-β) = Crd(180°-α)×Crd(180°-β)/2R - Crdα×Crdβ/2R
という公式が得られます。これは、cos(x+y)=cos x×cos y-sin x×sin y を意味しています。
二つの角の差の弦の長さ
- 図A
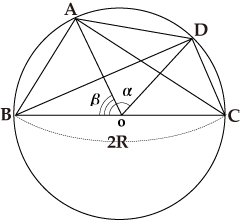 図で、∠BOD=αの弦BDの長さをCrd αと書くことにします。
図で、∠BOD=αの弦BDの長さをCrd αと書くことにします。
∠AOB=βとすると、∠AOC=180°-βですので、AC=Crd(180°-β)です。
∠AOD=α-βですので、AD=Crd(α-β)、
∠DOC=180°-αですので、DC=Crd(180°-α)となります。
二つの角の和の弦の長さ
- 図B
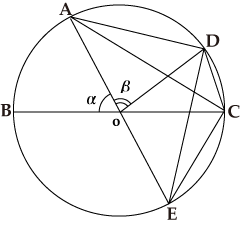 図で、∠AOB=αとすると、∠AOC=180°-αですので、AC=Crd(180°-α)です。
図で、∠AOB=αとすると、∠AOC=180°-αですので、AC=Crd(180°-α)です。
∠AOD=βとすると、∠DOE=180°-βですので、DE=Crd(180°-β)です。
また∠DOC=180°-α-β、∠COE=αですので、DC=Crd(180°-α-β)、CE=Crd αとなり、AD=Crd βと合わせてトレミーの定理を使います。


