第3章 家元制度 趣味としての和算
コラム 算額(難易度0)
算額は数学の問題が書かれた絵馬で、江戸時代になってから、神社仏閣に奉納されるようになりました。美しい図形を扱った問題が多く、ほとんどが彩色されています。現存するもので一番古い算額は、栃木県佐野市の星宮神社に天和3年(1683)に奉納されたものです。しかし、この算額は1975年に火災に遭って判読出来なくなり、現在は複製が掲げられています。次に古いとされるのは京都八坂神社に元禄4年(1691)に奉納されたもので、1993年には国の重要文化財に指定されました。算額の風習は江戸時代には非常に盛んであったそうで、明治時代まで続きました。しかし、以降はすたれ、また掲げられていた算額も破損などで取り払われたりして、現存するのは約1,000件(江戸時代のものは約400件)といわれます。
実際にどれくらい算額が作られたかについては、完全な記録はなく、算額を転載した本からどのような算額があったかをうかがい知ることができるのみです。算額について言及した最初の本は村瀬義益の『算法勿憚改(ふつだんかい)』(1673)といわれ、目黒不動に掲げられていた算額について記しています。算額を集めた最初の本は藤田貞資(1734-1807)の『神壁算法』で、寛政元年(1789)に刊行されました。寛政8年(1796)には増補版が『増刻神壁算法 下』と題して、また文化4年(1807)には息子の藤田嘉言(1772-1828)が続編として『続神壁算法』を刊行しました。主に藤田の弟子たちの算額を収録しています。中村時万(?-1881)の『賽祠神算』(1830)は写本でのみ流布しましたが、204件の算額を収録しています。
また、江戸時代には各地を旅して和算を教える遊歴算家と呼ばれる和算家がいました。そのうちのひとり山口和(c.1781-1850)は、文化14年(1817)から文政11年(1824)にかけての遊歴の記録を『道中日記』として残しました。彼はこの中に各地で見た算額の問題を324題書き写しています。ほかに、個別の神社に奉納された算額を記録した写本も多数残されています。
明治に入ると、和算は実践より数学史の対象として研究されるようになります。和算研究は和算書を解読することから進められました(コラム 明治以降の和算史研究)が、各地に残る算額に注目する研究者もいました。戦前期に全国に残る算額を調べて本にしたのは清水義雄(1896-1983)の『社寺奉納算額集』(1942)が最初で、141件の算額が記載されています。孔版印刷で68部しか印刷されなかったため、入手がむずかしくなっています。
戦後、各地に残る算額の調査が行われるようになります。和算研究家平山諦(1904-1998)は1960年代に山形、福島、千葉の算額調査結果を刊行しました。そのころ長野、茨城、新潟、埼玉、栃木の算額集も刊行されています。和算研究家下平和夫(1928-1994)は、三上義夫の『文化史上より見たる日本の数学』新版(1984)の付録として817件の現存算額の所在表を作りました。この仕事を引き継いだのは1970年代から愛知の算額調査を行っていた深川英俊(1943-)で、『例題で知る日本の数学と算額』(1998) に884面の現存算額、91件の復元算額の一覧表を作っています。さらに、現存しないが文献で確認される1,749面の算額の一覧も作りました。2005年には130件ほどの算額を集めた「庶民の算術展」が名古屋市科学館で開かれました。なお、算額の写真は「和算の館」( http://www.wasan.jp/ )というホームページで見ることができます。
算額は美しい図が描かれ、簡潔な式が答えとなる問題 が多く、深川英俊の本は英語でも出されていますので、海外の算額ファンも増えています。フランスでは G. Huvent: Sangaku; le myste`re des enigmes geome'triques japonaises (Paris, 2008) という算額の本が刊行されています。また、Japanese temple mathematical problems in Nagano Pref. Japan (Nagano City, 2003) のように英語で算額を紹介した国内の刊行物もあります。
また、最近では和算を扱った小説もたくさん書かれるようになりましたが、その中にしばしば算額の話が登場します。例えば、『算法少女』に題材をとった児童文学作家遠藤寛子の同名の小説(1973)は、主人公が算額の問題の解答が間違っていることを見つけることから始まっています。
遠藤寛子『算法少女』に出てくる算額の問題
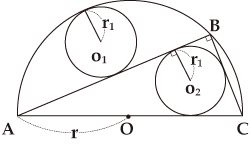 図で△ABCはOを中心とする半径rの半円に内接する直角三角形で、円O1と円O2は等しい半径r1を持ち、O1は弧
図で△ABCはOを中心とする半径rの半円に内接する直角三角形で、円O1と円O2は等しい半径r1を持ち、O1は弧![]() と線分ABに接する最大の円、O2は△ABCに内接する円です。この時、rとr1の関係を求める問題で、解答は腕試し問題Q11にあります。
と線分ABに接する最大の円、O2は△ABCに内接する円です。この時、rとr1の関係を求める問題で、解答は腕試し問題Q11にあります。
算額の問題は、このような図形の問題が多く、山本賀前(1811-?)の『算法助術』(1841)のような、数学的に美しい関係を集めた公式集も作られました。和算では、図形の中にまた図形を入れてその関係を調べる容術という分野があります。腕試し問題Q9~11にいくつかの例が入っていますので、そちらもご覧ください。
-

『神壁算法』
『神壁算法』の拡大画像を表示 -
『続神壁算法』
『続神壁算法』の拡大画像を表示 -

浅草観世音堂の算額の問題
『賽祠神算』の拡大画像を表示
『賽祠神算』


