幾何の問題
- 容術
- 算額には容術と呼ばれる、ある図形に別の図形をいくつも内接させる問題がよく取り上げられました。ここでは、特に円を用いる容術の例をみてみましょう。
| Q9 |
|
|---|---|
| ヒント | 三角形の面積と内接円の関係を使って考えてください。 |
| Q10 |
|
|---|
| Q11 |
|
|---|---|
| ヒント | 直角三角形に内接する円の半径に関する公式を使うとわかりやすくなります。 |
- 裁ち合せ
- コラム「ピタゴラスの定理」で、和算家は裁ち合せにより、ピタゴラスの定理を証明したことをお話ししました。中根彦循(1701-1761)は『勘者御伽双紙』(1743)の中で裁ち合せの例をいくつも紹介しています。
ここでは、裁ち合せを実際にやってみましょう。まず正方形2個分の長方形をハサミで切って正方形1個にしてみます。
図A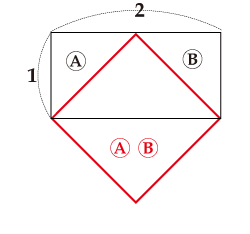
図B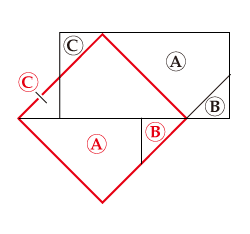
図C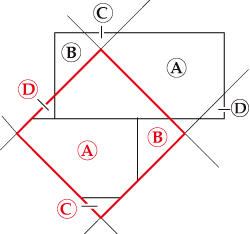
正方形2個分の長方形を裁ち合せて正方形1個にする
2個の場合は図Aのように簡単なやり方がありますが、実はこれ以外にもいくらでも切り方があります。図Aの切り方を平行移動した図Bや図Cを見ますと、確かにこの切り方でもよいことが確認できます。
次に、同じ大きさの3個の正方形を裁ち合せて1個の正方形を作ってみましょう。
| Q12 | 同じ大きさの3個の正方形をハサミで切って、1個の正方形を作りたい。どのように切ればよいでしょう。 |
|---|---|
| ヒント | 作りたい正方形の1辺の長さはどうなるでしょう。 |
三角形をハサミで切って長方形にするのは、図のように中点連結定理を使って簡単にできます。
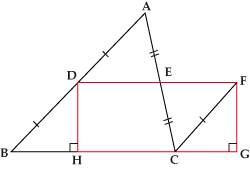
四角形を裁ち合せて長方形にすると面積の計算が簡単になるのですが、どう切ればよいでしょう。
| Q13 |
|
|---|
正五角形や正六角形にハサミを入れて正方形を作ることもできますので、一度チャレンジしてみてください。木村稔子『面積であそぼう』(国土社 1982)という本に解答が載っています。


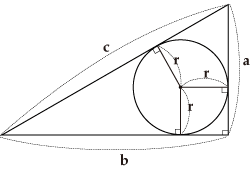 図のような3辺の長さがa,b,cの直角三角形の内接円の半径rを求めなさい。
図のような3辺の長さがa,b,cの直角三角形の内接円の半径rを求めなさい。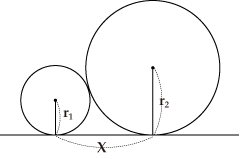 図のように直線上で接する二つの円があるとき、直線との接点間の距離を求める公式は容術でよく使われます。図のxを求める式を導いてください。
図のように直線上で接する二つの円があるとき、直線との接点間の距離を求める公式は容術でよく使われます。図のxを求める式を導いてください。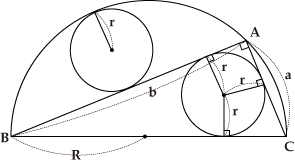 コラム
コラム


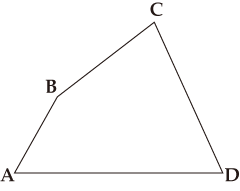 図のような四角形をハサミで切って長方形を作ってください。
図のような四角形をハサミで切って長方形を作ってください。

