第2章 関孝和
コラム ホーナー法(高次方程式の近似解法)(難易度3)
江戸時代の数学で行われた方程式の解法は、1819年にイギリスの数学者W.G.ホーナー(1786-1837) が発表(論文をD.ギルバートが代読)したものと同じであることが、明治以来、和算史研究家により指摘されてきました。明治に入って日本の大学で使われた方程式の教科書にI. Todhunter: Elementary treatise on the theory of equations, with a collection of examples (初版 1861)というイギリスの本があります。
この第18章はHorner's method と題され、ホーナー法が説明されています。これは高次方程式の数値解法で、組立除法を使って効率的に近似解を求めるアルゴリズムです。この組立除法による方程式の解法は13世紀の中国で行われており、それが我が国にも入ってきましたので、東洋では古くからホーナー法が行われていたといわれます。
組立除法は多項式f(x)を(x-α)で割った時の商と余りを計算する方法で、この余りはf(α)と等しくなる(剰余の定理)ので、高次多項式f(x)に対して少ない計算回数でx=αの値f(α)を計算する方法としても知られます。これを繰り返し行うと、f(x)のx=αでのテーラー展開の係数が得られます。その係数は、f(x)=0という方程式に対して、その根がすべてαだけ小さくなるように変換された方程式の係数となりますので、真の値を求めるために根を少しずつ近似してゆく方法として使うことができます。これがTodhunterが解説したホーナー法の要点で、これにニュートンの近似法(テーラー展開して、高次を無視する)を組み合わせると、早く近似解が計算されます。
-
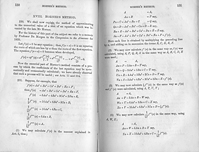
明治初期の東京大学で、菊池大麓が教科書として使った
Elementary treatise on the theory of equationsの拡大画像を表示
Elementary treatise on the theory of equations
ところで、古くから中国では算木を算盤の上で動かしながら計算を進めました。未知数を含む方程式も算木を動かしながら答えを出し、天元術と呼ばれました。13世紀に中国で書かれた秦九韶の『数書九章』は、最も発展した天元術が記され、そこでは-x4+763200x2-40642560000=0 という方程式が解かれています。
現在の普通の解き方では、まず両辺に(-1)を掛け、さらにy=x2 と置いて方程式を y2-763200y+40642560000=0 という2次方程式にすれば、
(y-381600)2-3816002+40642560000=0
(y-381600)2=104976000000
y-381600=±324000
y=381600±324000
y=705600 or 57600
![]() 、 従って x=±840 or ±240 が解
、 従って x=±840 or ±240 が解
という風に解けます。
しかし天元術では全く違う方法で解きます。それは、これから説明するように、方程式の解を大きな位から順に求めてゆく方法で、『数書九章』ではまず百の位は800、次に十の位は40、そして840がちょうど解になると記されています(しかし、もう一つの解である240のことは記されていないようです)。
-

『算学秘要』から「天元術図解」
『算学秘要』のライブラリーへ移動
方程式 x(x+5)=204 を解いて、解x=17, 12を得ています。
国立国会図書館デジタルコレクション
組立除法とは
f(x)=x5 + 2x4 + 3x3 + 4x2 + 5x + 6 について f(15) を計算する場合、式にあるとおりに計算すると、掛け算と足し算で合計19回の演算が必要になります。ところが、まず f(x)を(x-15)で割る計算をすると、剰余定理から、その余りがf(15)の解になります。その計算を定型的に行うのが組立除法で、8回の演算ですみます。まず下図の赤字のように数字を書き並べ、順番に演算を進めて行きます。

最下段の左から5つの数字は f(x)を (x - 15)で割った時の商の係数を表し、右端の数字が余りを表しています。すなわち、f(x)=(x-15)(x4 + 17x3 + 258x2 + 3874 x+ 58115) + 871731であり、f(15)=871731と分かります。
何故こういう結果になるかは、組立除法(確認)で説明しています。
組立除法の繰り返しとテーラー展開
f(x) = x3 + 2x2 + 3x + 4 を(x-1)で割る場合について組立除法を繰り返してみます。
まず、f(x) =(x-1)(x2 +3x + 6) + 10 であることがわかります。
さらに、(x2 +3x + 6) を(x-1)で割ると、x2 +3x + 6 = (x-1)(x + 4) + 10 =(x-1){ (x-1) + 5} + 10 となります。
従って
f(x) = (x-1)[ (x-1){ (x-1) + 5} + 10] + 10 = (x-1)3 + 5 (x-1)2 + 10 (x-1) + 10 となります。
組立除法を繰り返し行いますと
このようになり、青い数字が f(x) を(x-1)の冪(ベキ。累乗。)で書き変えた式の係数を表しています。この多項式の変換は、実はf(x)を x=1でテーラー展開したことと等しく、実際にテーラー展開してみますと、
![]()
ですが、![]()
より、f(x)= 10+ 10 (x-1) + 5 (x-1) 2 + (x-1)3となって、同じ結果となります。
このアルゴリズムを方程式の数値解法に応用したのがホーナー法です。
方程式の変換
f(x) =0 として x3 + 2x2 + 3x + 4 = 0 という方程式Aを考えることにします。前項より、この方程式は (x-1)3 + 5 (x-1)2 + 10 (x-1) + 10 = 0 とも書きかえられます。 y = x-1とおくと y3 + 5y2 + 10y + 10 = 0 という方程式Bとなり、x = 1 + y ですので、このyについての方程式Bの解に1を加えた数は方程式Aの解となります。このことをTodhunterは前出の教科書で方程式の変換と呼んでいます。
例 この方法で x2 + x-12 = 0 ・・・(1) を解いてみましょう。
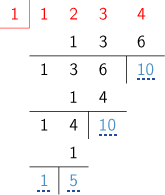
x=1でテーラー展開した時の係数を求める組立除法を行いますと、
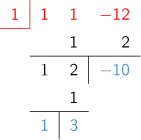
ですので、方程式は (x-1)2 + 3(x-1)-10 = 0 と変換されます。y = x-1とおいて方程式をy2 + 3y-10 = 0 ・・・(2) と書き変えますと、この解がわかれば、その数に1を加えた数が(1)の解です。
(2)についてもy=1でテーラー展開した時の係数を求める組立除法を行いますと、方程式は (y-1)2 + 5(y-1)-6 = 0 と変換されます。y-1=1とおいて方程式をz2 + 5z-6 = 0 ・・・(3) と書き変えますと、(3)はz=1 が解であることが明らかです。すると(2)の解はy=z+1=1+1=2 であり、(1)の解は x=y+1=2+1=3 であることが分かります。(z=-6も解ですが、するとx=-4になります。和算では、負の解を扱いません。)
和算では算木を使って、このアルゴリズムで高次方程式の解を求めました。
Todhunter は 2x3-473x2-234x-711 = 0 をホーナー法で解く例を説明しています。 f(x) = 2x3-473x2-234x-711としますと、f(100) = -2754111、f(200) = -2967511、 f(300) = + 11359089 と求められますので、f(x)=0となる解は200と300の間にあります。そこで組立除法で x = 200でテーラー展開して、f(x)= 2(x-200)3 + 727(x-200)2 + 50566(x-200)-2967511と変換します。
さらに、余りが0に近づくよう見当をつけて、f(x)= 2(x-230)3 + 907(x-230)2 + 99586(x-230)-742231、
f(x)= 2(x-237)3 + 921(x-237)2 + 106033(x-237)-0 と続けるとf(237)=0 ですので、解が x=237 であることが分かります。組立除法の実際については 腕試し問題Q7をご覧ください。
-

『算法少女』より5次方程式の問題
『算法少女』のライブラリーへ移動
4021608000 - 1908102200x + 361134200x2 - 34070206x3 + 1601620x4 - 30000x5 = 0 という問題で、答えは10, 40/3, 2501/250, 201/20 であるが、解き方は秘密であるとしています。(「+ 1601620」は『算法少女』本文では「- 1601620」とあり、誤植)
国立国会図書館デジタルコレクション
方程式の近似解法
これまでは方程式の解が整数の場合をみてきました。実際には、ホーナー法は解が無理数で有る場合に、解の近似値を求める方法として使われます。
x2-2 = 0 の正の解は![]() ですが、小数で表すと 1.41421356... と無限に続きます。ホーナー法を使うことで、解の数値を1桁ずつ求めることができます。
ですが、小数で表すと 1.41421356... と無限に続きます。ホーナー法を使うことで、解の数値を1桁ずつ求めることができます。
f(x)=x2-2 = 0 について、方程式がどう変換されて行くかを見てみましょう。厳密な解に到達する変換は![]() ですが、組立除法で1桁ずつ変換して、余り部分がより0に近づくようにしていくと、f(x)=(x-1)2 + 2(x-1) -1 = (x-1.4)2 + 2.8(x-1.4) -0.04 = (x-1.41)2 + 2.82(x-1.41) -0.0119 = (x-1.414)2 + 2.828(x-1.414) -0.000604 = (x-1.4142)2 + 2.8284(x-1.4142) -0.00003836 となってゆきます。これぐらい続けますと、(x-1.4142)2が非常に小さな数字となり、以下の桁は2.8284(x-1.4142) -0.00003836 =0 を計算するだけで求められ、x-1.4142 = 0.00003836/2.8284 = 0.00001356243 と、小数点以下9桁まで正しい数値が得られ(赤字が誤り部分)、もう1桁組立除法を続けますとf(x)=(x-1.41421)2 + 2.82842(x-1.41421) -0.0000100758 となって、x-1.41421 = 0.0000100758/2.82842 = 0.000003562377 と、小数点以下11桁まで正しい数値が得られます(赤字が誤り部分)。
ですが、組立除法で1桁ずつ変換して、余り部分がより0に近づくようにしていくと、f(x)=(x-1)2 + 2(x-1) -1 = (x-1.4)2 + 2.8(x-1.4) -0.04 = (x-1.41)2 + 2.82(x-1.41) -0.0119 = (x-1.414)2 + 2.828(x-1.414) -0.000604 = (x-1.4142)2 + 2.8284(x-1.4142) -0.00003836 となってゆきます。これぐらい続けますと、(x-1.4142)2が非常に小さな数字となり、以下の桁は2.8284(x-1.4142) -0.00003836 =0 を計算するだけで求められ、x-1.4142 = 0.00003836/2.8284 = 0.00001356243 と、小数点以下9桁まで正しい数値が得られ(赤字が誤り部分)、もう1桁組立除法を続けますとf(x)=(x-1.41421)2 + 2.82842(x-1.41421) -0.0000100758 となって、x-1.41421 = 0.0000100758/2.82842 = 0.000003562377 と、小数点以下11桁まで正しい数値が得られます(赤字が誤り部分)。
実は、この方法で平方根を求めるのは、開平法の筆算と同じことを行っています。
平方根の近似値を小数の形ではなく、![]() のように分数の形で求めることも行われてきました。これについては腕試し問題Q8をご覧ください。
のように分数の形で求めることも行われてきました。これについては腕試し問題Q8をご覧ください。


