n進法

3反4畝16歩や1時間35分25秒、23度22分21秒のように、長さや面積、時間、角度などでは10進法でない単位が一緒に使われています。こうした単位表示がされた数の間の計算には注意が必要になります。『塵劫記』の例を見てみましょう。

Q1	縦37間、横28間の長方形の面積を求めよ。(『塵劫記』二、第四「検地のこと」より)
ヒント	古代より、長さの単位は6尺が1間、60間が1町、面積の単位は1間2=36尺2が1歩、1町2=3,600間2が1町（面積の）など6の倍数の進法が土台でした。これは、条理制で計算しやすい単位を使ったためです。また、1町のを1段(反)、1段のを1畝と呼ぶ10進法も併用されています。しかし、時代により換算が変わり、太閤検地以降、もともと1段(反)=360歩であった換算式が1段=300歩、1畝=30歩という換算式に変更されました。『塵劫記』では、後者の換算式を使っています。

解答はこちら

整数

合同式

まずは連立合同式の基本的問題です。中国式剰余定理をそのまま使ってください。

Q2	x≡a (mod 5) & x≡b (mod 11) & x≡c (mod 13)の一般解を求めなさい。
ヒント	5,11,13は互いに素ですので、まず、11×13の倍数で5割ると1余る数などを探します。

解答はこちら

関孝和は『括要算法』で様々な連立合同式を扱いました。割る数が互いに素な整数の場合は、中国式剰余定理の通り機械的に計算すればよいのですが、次の問題のような公約数を持つ場合はどうすればよいでしょうか。

Q3	36で割ると2余り、48で割ると14余る数は何か。
ヒント	36と48の最大公約数は12で、36と48は互いに素ではありません。x≡2 (mod 36)となるxは36の約数aについてx≡2(mod a)となります。同様にx≡14 (mod 48)となるxは48の約数bについてx≡14(mod b)となります。このようなaとbが互いに素であれば中国式剰余定理が使えます。

解答はこちら

冪和

中国の数学書に垜術と呼ばれる級数計算があり、我が国でも関孝和が『括要算法』で取り上げています。方垜という

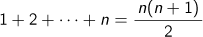
や

、

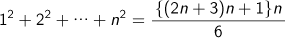
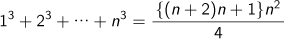
などの公式が記され、さらに衰垜という面白い級数の公式を求めています。

衰垜の部分。1+(1+2)+(1+2+3)+…という三角衰垜や、三角衰?を順に足す1+{1+(1+2)}+{1+(1+2)+(1+2+3) }+…という再乗衰垜、再乗衰垜を順に足す三乗衰垜などの公式が取り上げられています。

衰垜には際立った規則性がありますので、それを問題にしてみましょう。

Q4	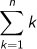と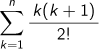をnの式で表し、それから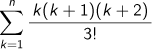がどのような式になるかを予想してみましょう。
ヒント	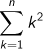がわかれば、計算で求めることができます。

解答はこちら

Q5	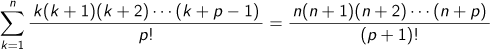となることを数学的帰納法で証明してみましょう。

解答はこちら

Q6	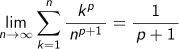となることを証明してみましょう。
ヒント	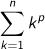はnの(p+1)次式となり、n⇢∞ではp次以下の係数は無視することができます。

解答はこちら

組立除法

ホーナー法は方程式の解を級数の形で得ることにも使えます。和算家たちは2次方程式の解をホーナー法で級数展開した形の解を求めました。

解答はこちら

有理数近似

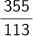は3.14159292でπに近い数字です。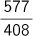は1.414215686で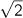に近い数字です。近似値を求める場合、こうした分数を使うと桁数が少ない計算で済むので、和算でもよく利用されました。それでは、ある無理数に非常に近い有理数をどうしたら探し出せるでしょうか。一つの方法をご紹介してみましょう。

Q8	2次方程式x2-x-1=0 の解はです。同じ方程式x2=x+1の両辺をxで割るとx=1+1/xとなりますが、この方程式の正の解はどういう分数で近似されるでしょう。
ヒント	連分数と呼ばれる分数です。

解答はこちら