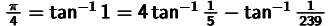コラムなぜ、π/4＝tan-1乗1＝4tan-1乗(1/5)-tan-1乗(1/239)　となるのか

角度αについて

$tanα=1/5 (tan-1乗(1/5)=α)$

であるとします。すると、

$tan2α = 2tanα/(1-tan2乗α)={2×(1/5)}/{1-(1/5)2乗} = 10/24 =5/12$

となり、これを繰り返すと

$tan4α= 2tan(2α)/(1-tan2乗(2α)) ={2×(5/12)}/{1-(5/12)2乗} = 120/119 = 1+1/119 = tan(π/4)+1/119$

です。

ところで、tanの加法定理

$tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)$

により、

$tan(4α-π/4)=(tan4α-tan(π/4)/(1+tan4α×tan(π/4))=(1/119)/(1+120/119))=1/239$

となりますので、

$tan-1(1/239)= 4α-π/4= 4tan-1(1/5)-π/4$

すなわち

$π/4＝4tan-1(1/5)-tan-1(1/239)$

が導かれます。この

$tanα=1/5$

の時、

$tan4α= tan(π/4)+1/119$

が成り立つことはロンドンの天文学者J. マチンが発見し、彼はこの関係と

$tan-1x=x-x3/3+x5/5-x7/7+ …$

を使って、1706年に円周率を小数点以下100桁まで計算しました。8桁の電卓を使って、

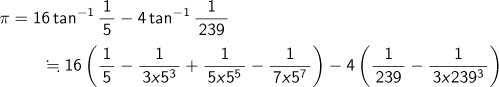
$π＝16tan-1(1/5)-4tan-1(1/239)≒16(1/5-1/3x53+1/5x55-1/7x57)-4(1/239-1/3x2393)$

を計算してみますと、3.1415918 という数字が得られます。

その後も

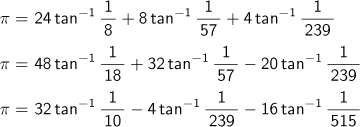
$π＝24tan-1(1/8)+8tan-1(1/57)+4tan-1(1/239)　　,π＝48tan-1(1/18)+32tan-1(1/57)-20tan-1(1/239)　　,π＝32tan-1(1/10)-4tan-1(1/239)-16tan-1(1/515)$

などの関係式が見つかり、さらに大きな桁の円周率計算が行われました。

第2章関孝和