第4章 実学としての和算
コラム 測量の方法(難易度0)
測量は、田畑の面積を計算する方法として古代から行われてきました。また、都市造りや建築、あるいは天体観測や暦作りに欠かせない技術でもありました。幾何学(geometry)とは土地(geo)の測量(metry)から作られた言葉で、測量は数学の一分野のルーツです。「幾何」という言葉は、幾何学の祖ユークリッドの『原論』が漢訳されたとき、geoに中国音を充てたものでした。ここでは、基本的な測量の方法について解説してみましょう。
検地
我が国では7世紀に「班田収授の法」が施行されることで、中国の数学書『九章算術』に基づいて、田の面積が調べられるようになりました。面積の単位も歩、段、町という中国の単位が使われています。面積は長さを測って計算で求め、古代では1辺が6尺の正方形の面積を1歩としました。大きな面積は1段(=360歩)、1町(=10段) という単位も使い、1辺が60間=360尺の正方形の面積が1町でした。1町は長さの単位としても使われ、60間=360尺のことも1町と呼ばれますが、太閤検地以降、1辺が1町の正方形の面積は、1町より少し大きくなります。このように、時代により長さの基準や名称が変わっていますので、注意が必要です。1間の長さも6尺と決まっていたわけではなく、6尺5寸や6尺3寸の時代もありました。1歩は1坪とも呼ばれますが、明治の度量衡法で約3.3m2の面積とされました。1坪は1辺の長さが1間の正方形の面積ですので、1間は約1.8mの長さです。1尺は1/6の30.3cmとなります(正確には1尺=10/33m)。
ところで、『九章算術』では冒頭の第一章「方田」で田の面積計算を扱っており、「方田」(長方形)、「圭田」(三角形)、「箕田」(台形)、「円田」(円)、「環田」(ドーナツ形)、「弧田」(弓形)の面積の計算公式が示されています。ここでは円周率は3が用いられています。日本の『塵劫記』は「検地のこと」という章で面積を扱っており、まず面積の単位の換算をしています。(腕試し問題Q1を参照)そして、正三角形、正六角形、正八角形、平行四辺形などの面積計算のほか、曲線の図形を多角形で近似して面積を出しています。この方法が、実際の検地で使われた方法のようです。田に十字形に縄を張って、田と等積の長方形を作ることで、面積を計算します。この縄の張り方が万尾時春『勧農固本録 下』(1725)に図示されています。
長方形からだいぶ離れた四角形の面積については、二つの三角形に分けて計算する方法もあり、現存最古の数学書といわれる『算用記』(c.1600)に記されています。
三角形の面積は3辺の長さを測ると、ヘロンの公式を用いて計算できるのですが、この方法が一般的に使われることはなかったようです。また、四角形の面積についてはコラム「ピタゴラスの定理」で出てきた裁ち合せを使って、長方形に直して計算する方法もあります。これについては腕試し問題Q13をご覧ください。
-

十字の張り方の図
『勧農固本録 下』の拡大画像を表示
『勧農固本録 下』 -
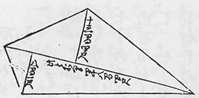
「けんちさをのうちやう」の図
『算用記』の拡大画像を表示
『算用記』
山の高さ
さて、土地の辺の長さは縄などを使って直接測れますが、山の高さは直接には測れません。しかし、古代から山の高さは測られてきました。どのようにして測ったのでしょうか。
前出の古代中国の数学書『九章算術』に山の高さを求める例が出ています。山の手前にある木の天辺と山頂がちょうど重なる位置から木までの距離と山までの距離を測り、直角三角形の相似を使って計算する方法です。
山の高さの測り方
 図では、人の視線で木の天辺と山頂がちょうど重なっています。
図では、人の視線で木の天辺と山頂がちょうど重なっています。
DEの長さ、QEの長さ、BDの長さ、AEの長さがわかると、△ABCと△BPR、△APSが相似であることから、PRの長さ、あるいはPSの長さを計算で求めることができます。
日本でも古代から山の高さは測られており、『出雲風土記』には、測量法は書かれていませんが「神名火山、郡家の東北のかた九里四十歩なり。高さ二百三十丈、周り十四里なり」とか「足日山...高さ百七十丈、...足高野山...高さ百八十丈、...」などと記載されています。これらの山は島根県松江市の朝日山、経塚山、本宮山のことで、高さはそれぞれ342m、315m、279mです。中国から入ってきた測量法で測ったものと思われますが、経塚山と本宮山で高さが逆の結果となっており、誤差の大きな測量であったと思われます。
この比較のための木の代わりに四方矩(しほうのかね)と呼ばれる器具を使うことで、どこからでも山の高さが測れるようになります。この器具は、正方形の板の一つの頂点からおもりが糸でつりさげられ、さらに各辺に長さの目盛が打たれているもので、一辺を測りたい目標に向けて傾け、その時の糸の位置の目盛を読むようになっています。その様子は享保13年(1728)に書かれた松宮観山『分度余術』に図示されています。
これを使うと、山までの距離がわからない場合でも、山頂の真下を通る直線上の2点で測定することで、山頂の真下までの距離を計算で求めることができます。
山までの距離がわからない場合
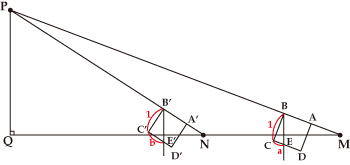 図で正方形ABCDを1辺の長さが1の四方矩とします。
図で正方形ABCDを1辺の長さが1の四方矩とします。
地点Mでの目盛a、地点Nでの目盛bを測定し、MNの距離Cを測定したとすると、△MPQと△BCEが相似であり、△NPQと△B’C’E’が相似であることを使って、PQの長さを計算で求めることができます。公式は![]() です。
です。
この頃(1727年)、富士山の高さが測られ、メートル法に直すと約3,886mという結果が得られています(現在は、3,776mとしています)。
平板測量
測量術には、オランダ人から伝わったということで紅毛流と呼ばれるものがあります。長崎の与力、樋口権右衛門(小林義信)が17世紀半ばに医師カスパルから学んだとされる技術が伝わり、清水貞徳(1645-1717)が規矩術(きくじゅつ)として体系化しました。規はコンパス、矩は定規のことで、平らな板の上に置いた紙の上に図を書いて、それをもとに計算するというものです。和算資料ライブラリーの松宮観山『分度余術』、河原貞頼『規矩要法口傳私録』、細井広沢『秘伝地域図法大全』などに、この紅毛流測量の方法について具体的な記述があります。
ここでは、川向うの地点までの距離の測量方法を以下の図で説明してみましょう。
川向うの地点までの距離の測量
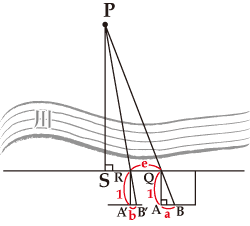 図で四方矩を水平に置いて地点Qで△QABが作図され、線分ABと並行な直線上を移動して、地点Rで△RA’B’が作図されたとすると、QRの長さと、QA、AB、RA’、A’B’の長さがわかれば地点Pまでの距離を計算することができます。
図で四方矩を水平に置いて地点Qで△QABが作図され、線分ABと並行な直線上を移動して、地点Rで△RA’B’が作図されたとすると、QRの長さと、QA、AB、RA’、A’B’の長さがわかれば地点Pまでの距離を計算することができます。
QA=RA’=1、AB=a、A’B’=b、QR=cとすると![]() です。
です。
特に地点Sまで移動して、QSの長さdを測ると![]() となります。
となります。
三角関数表を使う
18世紀には、角度を測定する装置や三角関数表が入ってきました。これにより西洋流の測量が本格化し、上記の規矩術でも角度を測って三角関数表で距離を計算する方法が述べられています。山の高さの測量は角度を使うと次のような計算法になります。
山の高さの三角関数での計算
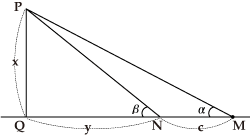 図で∠PMQ=α、∠PNQ=β、MN=cを測定結果とします。PQ=x、QN=yとおくと、
図で∠PMQ=α、∠PNQ=β、MN=cを測定結果とします。PQ=x、QN=yとおくと、
![]() より、
より、![]()
すなわち ![]() となり、
となり、
山の高さが計算されます。
また、川向うの地点までの距離は、直角三角形となる位置関係でなくても、2点を選んで、2点間の距離と目標地点との角度を測ることで、以下の図のように、各点から目標点までの距離を計算することができます。
三角測量
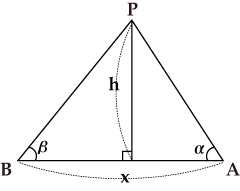 図で∠PAB=α、∠PBA=β、AB=xを測定結果とします。
図で∠PAB=α、∠PBA=β、AB=xを測定結果とします。
すると、x=PA cos α+PB cos βですが、h=PA sin α=PB sin βなので、
![]() より
より
![]() となります。同様に
となります。同様に
![]() となり、PA、PBの長さを計算することができます。
となり、PA、PBの長さを計算することができます。
これが三角測量の原理で、距離の測量が一回で済むため、明治になって各地に基準となる三角点が設置されました。
地図を作る
測量を繰り返すことで地図を作ることができます。和算資料ライブラリーの宮井安泰『国図携要』は地図作りのための測量マニュアルです。地図作りとしては伊能忠敬(1745-1818)が有名ですが、彼は導線法という方法で測量し、海岸線や道路の曲り具合を正しく地図に描きました。
導線法
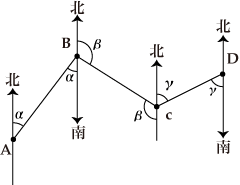 図でABの距離と角α、BCの距離と角β、CDの距離と角γを測量しながら前進していく測量法を導線法と呼びます。∠ABC=π+α-βなのでACの距離が求まり、∠BACや∠BCAが計算できます。
図でABの距離と角α、BCの距離と角β、CDの距離と角γを測量しながら前進していく測量法を導線法と呼びます。∠ABC=π+α-βなのでACの距離が求まり、∠BACや∠BCAが計算できます。
しかし、距離の測量は誤差が大きく、角度の測定の方が正確にできますので、∠BACと∠ABCとABの距離からBCやACの距離を出すのが三角測量です。
彼の測量法には誤差を小さくするための各種の工夫がされています。まず、象限儀を用いて北極星の高度を測ってその地点の緯度を求め、補正に利用しました。また、坂道の場合、距離が長めに測られるので、勾配を小型の象限儀で測って、三角関数表で平面距離に換算しました。完成した「大日本沿海輿地全図」は非常に正確で、明治に入ってからも使われました。
- コラム 測量グッズ(難易度0)



