解析の問題
- 円周率
- ここでは無限が登場する問題を考えてみましょう。円のような曲線の長さ、それが囲む面積などは現在では解析学で取り扱われます。その発想は曲線を細かく分割して、折線で近似する方法で、古代から行われてきました。例えば、円の面積がS=πr2となることを和算家は図のようにして直観的に導いています。
なかでも古代ギリシアのアルキメデスは円や螺旋、放物線などの曲線を研究しました。彼は円周率の大きさについて![]() という結論を得ていますが、どのような計算をしたのでしょうか。
という結論を得ていますが、どのような計算をしたのでしょうか。
アルキメデスは最初に、円の面積と等しい面積の直角三角形は、1辺の長さが円の半径と等しく、それと直角に交わる辺の長さが円周と等しいとします。これは図Aのように考えたといわれます。
図A アルキメデスによる円の面積の図示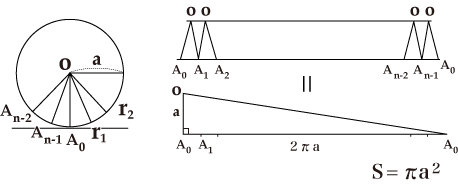
ここでは彼の計算を体験してみましょう。
図Bのように円に内接する正六角形と外接する正六角形から出発して、正十二角形、正二十四角形と細かくしていった極限が円になると考えるわけです。
図B 円に内接・外接する正六角形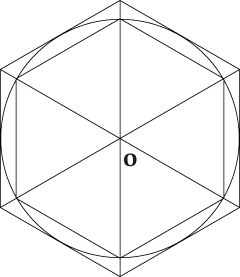
外接する正六角形の1辺の長さと正十二角形の1辺の長さの関係を求め、これを3度繰り返すと正96角形の1辺の長さが求まります。これはかなり面倒な計算ですが、古代数学の偉業に敬意を表して、それを問題としてみましょう。
| Q14 |
|
|---|---|
| ヒント |
同様の方法でアルキメデスは半径の円に内接する正96角形の周の長さは![]() より大きいことを証明し、
より大きいことを証明し、![]() という結論を得ました。『世界の名著9 ギリシアの科学』(中央公論社 1972)に「円の計測」という表題で邦訳があります。
という結論を得ました。『世界の名著9 ギリシアの科学』(中央公論社 1972)に「円の計測」という表題で邦訳があります。
日本で円周率の計算を行った関孝和は『括要算法』巻利で、まず、1辺の長さが1の正三角形から正二十角形の外接円と内接円の半径を計算し、それらの方程式を導きました。
次に、彼は『括要算法』巻貞で直径1の円に内接する正四角形から順に正八角形、正十六角形の周の長さを計算し、最後の正131,072角形の周の長さは3.1415926532…と計算しました。これも大変な計算量で頭が下がります。
- 円の三等分
- 最後に円に関する面白い問題を取り上げておきましょう。丸いケーキにナイフを入れて三等分したいが、どう切ればよいかという問題があります。ふつうは図Aのように切りますが、図Bのように切れれば中心を求める必要がありません。ではどこを切ればよいでしょう。
| 図A | 図B |
|---|---|
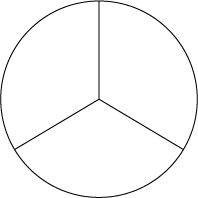 |
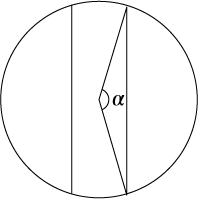 |
| Q15 | 図Bで角αの大きさは何度でしょう。 |
|---|---|
| ヒント | 超越方程式になりますので、数値計算でしか解けません。表計算ソフトなどを使って、近似解を求めてください。 |
この問題は和算家たちがよく取り上げ、吉田光由『新編塵劫記』(1641)に遺題として載ると、山田正重『改算記』(1659)や磯村吉徳『算法闕疑抄』(1659)などが解答を載せました。三宅賢隆『具応算法』(1699)はかなり細かい数字を載せています。



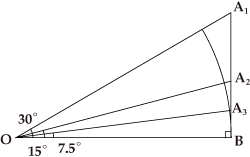 図で
図で