代数の問題 解答
n進法
| A1 |
|---|
整数
合同式
| A2 | 5,11,13は互いに素なので中国式剰余定理を使います。 11×13=143の倍数で 5で割ると1 余る最小の数は57×5+1=286、 5×13=65の倍数で11で割ると1余る最小の数は59×11+1=650、 5×11=55の倍数で13で割ると1余る最小の数は38×13+1=495ですので、x≡286a+650b+495c (mod 715) が一般解。 |
|---|
| A3 | x≡2(mod 36),x≡14(mod 48)で、36=22×32, 48=24×3 なので、36の約数aと48の約数bで、互いに素となるものはa=32とb=24です。すると、x≡2(mod 36)であるxはx≡2(mod 9)を満たし、一方x≡14(mod 48)であるxはx≡14(mod 16)を満たし、(9,16)=1。中国式剰余定理からx≡2(mod 9),x≡14(mod 16)の解は x≡p(mod 9x16)の形をしており、pは16の倍数で、9で割ると 2余る数である128と、9の倍数で、16で割ると 14余る数である270の和=128+270=398から9×16=144を順に引いてゆくと254,110となり、解はx≡110(mod 144)。 |
|---|
冪和
| A4 |
n3+3n2+3n=(n+1)3-1={(n+1)3-n3}+{n3-(n-1)3}+…+{33-23}+{23-13}
したがって、
となります。 |
|---|
| A5 |
したがって、n=m+1の時も成り立つので、あらゆるnについて成立します。
こうした関係式はすでに14世紀中国の数学書である朱世傑の『四元玉鑑』で取り扱われています。
|
|---|
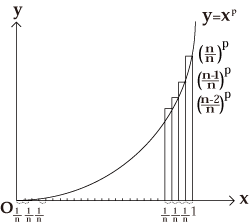
| A6 | Q5 で確認した
この問題は
と同じものです。 |
|---|
組立除法
| A7 |
解をpの冪級数で表すため、組立除法を使って、1次の係数から順番に高次の係数を求めていきます。方程式の定数項を小さくしていくことが目的ですので、まず定数項pが消えるようにp/2を最初の近似とすると、以下の組立除法となります。
これで、元の方程式を(x-p/2)2+(-2+p)(x-p/2)+p2/4=0 に変換したことになります。次にp2/4が消えるようにp2/8を2番目の近似とすると、以下の組立除法となります。
次にp3/8が消えるように、p3/16を3番目の近似とすると以下のようになります。
次に5p4/64が消えるように、5p4/128を4番目の近似とすると以下のようになります。
すると次の項は7p5/128を2で割った7p5/256であることがわかり、ここまでで、x=p/2+p2/8+p3/16+5p4/128+7p5/256+…という解の近似値を求めたことになります。 |
|---|
有理数近似
| A8 | 右辺の xを1+
と無限に続く式ができます。これは
という形の無限に続く分数がx=1+
、すなわち
となります。 このように
の形の分数を連分数と呼びます。
のように少しずつ正確な値へと近づいてゆきます。この分子と分母の数は、「次の分母=前の分子」、「次の分子=前の分母+前の分子」という関係があり、以下、 |
|---|



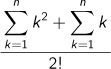 として計算できます。そして、
として計算できます。そして、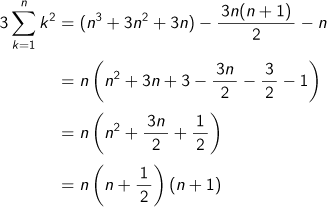
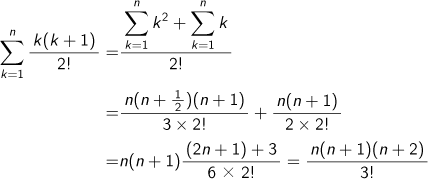
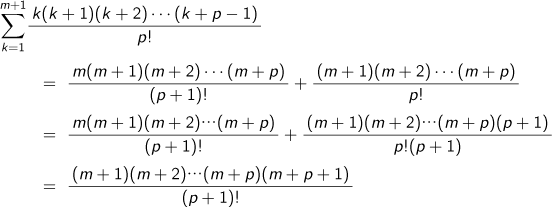
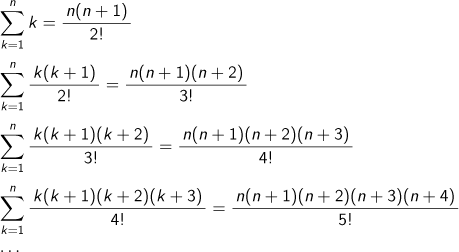
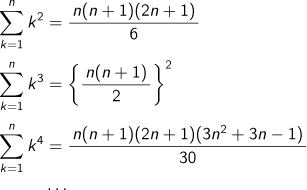
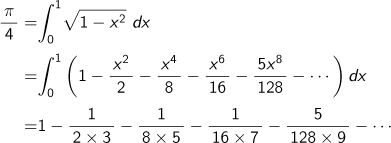
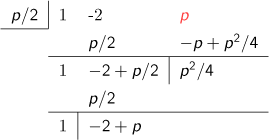
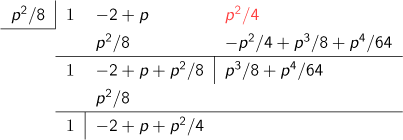
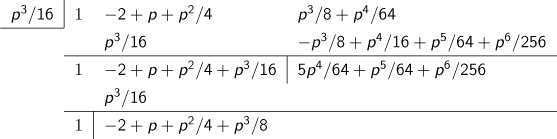

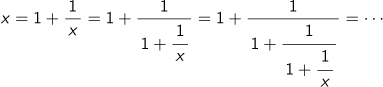
![1+1/[1+1/{1+1/(1+…)}]](/math/s1/images/a8_2.gif)
![(1+√5)/2=1+1/[1+1/{1+1/(1+…)}]](/math/s1/images/a8_4.gif)
![(√5)/2=1/2+1/[1+1/{1+1/(1+…)}]](/math/s1/images/a8_5.gif)
![a+1/[b+1/{c+1/(d+1/…)}]](/math/s1/images/a8_6.gif)
![1+1/(1+1)=3/2 、1+1/{1+1/(1+1)}=5/3、 1+1/[1+1/{1+1/(1+1)}]=8/5](/math/s1/images/a8_8.gif)

