解析の問題 解答
円周率
| A14 | 以下は、アルキメデスのたどった論理を少し現代的な表記にしてあります。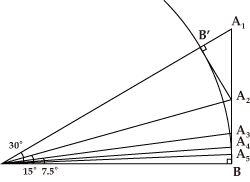 図で アルキメデスは、この論法をA3B、A4B、A5Bにも適用して、 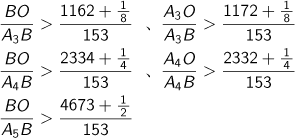 を計算しました。この逆数をとって96倍しますと外接正96角形の周の長さをBOで割った値は となり、円周は外接正96角形の周より短いので |
|---|
円の三等分
| A15 |
円の三等分はほかにもいろいろな方法があります。以下に二つの例を挙げておきますので、3等分になっていることを確かめてみてください。
|
|---|

| A14 | 以下は、アルキメデスのたどった論理を少し現代的な表記にしてあります。 図で アルキメデスは、この論法をA3B、A4B、A5Bにも適用して、 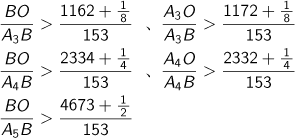 を計算しました。この逆数をとって96倍しますと外接正96角形の周の長さをBOで割った値は となり、円周は外接正96角形の周より短いので |
|---|
| A15 |
円の三等分はほかにもいろいろな方法があります。以下に二つの例を挙げておきますので、3等分になっていることを確かめてみてください。
|
|---|